Swift Algorithms: Getting Started
- The Tech Platform

- Feb 15, 2021
- 14 min read
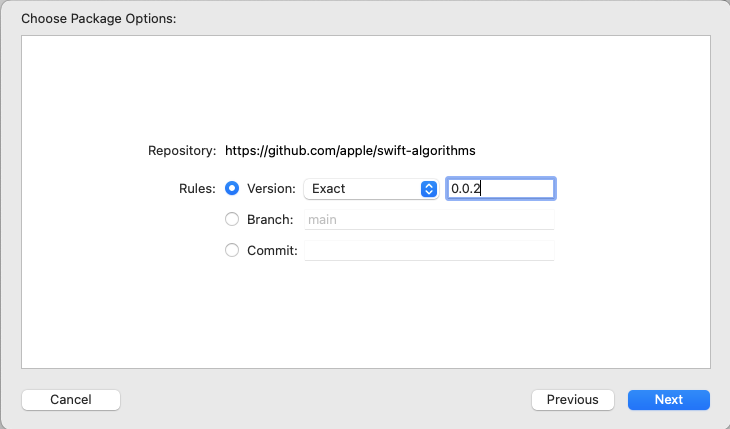
You need to install the Swift Algorithms package through the Swift Package Manager. In Xcode, choose File ▸ Swift Packages ▸ Add Package Dependency. In the text field, add the URL https://github.com/apple/swift-algorithms and click Next. Then, on the last screen, specify Exact as the version type and 0.0.2 as the version. Now, click Next
Click Finish on the final screen.
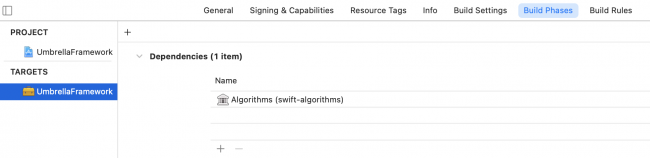
Next, select the project file from the Project navigator, then select the UbrellaFramework target. On the Build Phases tab, add Algorithms to the Dependencies list.
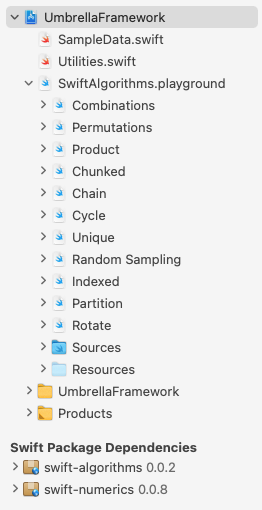
Feel free to look at the starter project in the Project navigator.
The project consists of a framework and a collection of playground pages. You’ll use each page of the playground to showcase a different part of Swift Algorithms. You’ll also find SampleData.swift with some mock data, along with Utilities.swift, which contains some helper methods.
As a small aside, you may be asking yourself why this framework isn’t part of the Swift standard library. If it were, its updates would be tied to OS updates. But the intention of this framework is to evolve quickly and separately from Xcode and OS updates.
Now, without further ado, it’s time to dive in to the algorithms!
Working With Combinations
Combinations is a mathematical term that describes the possible combinations of a set of items from a larger set without duplication of any items and with complete disregard to ordering.
If you have a set consisting of the three items — “A”, “B” and “C” — you can have three possible combinations choosing any two of those three:
“A” + “B”
“A” + “C”
“B” + “C”
The set “B” + “A” is identical to “A” + “B”, since the order doesn’t matter. With the same example, if the size of the combination’s set is three, you’ll only have one possible combination: “A” + “B” + “C”. This is exactly the same as the main set.
Consider calculating the possible number of combinations with a large set of five, choosing any two items. This is written as 5 C 2.
It’s calculated as:
5 × 4 × 3 × 2 × 1 / (3 × 2 × 1) × (2 × 1)To explain it in a more convenient way:
Factorial(5) / Factorial(5 - 2) × Factorial(2).Using the factorial of a number means you recursively multiply a number with the number below it until you reach one. The sample project already has the implementation you need for factorial().
Open SwiftAlgorithms.playground and, on the Combinations playground page, add the following:
func numberOfCombinations(_ total: Int, setSize: Int) -> Double {
return total.factorial() /
((total - setSize).factorial() * setSize.factorial() )
}
This new function will calculate the number of possibilities for you. Try it with a few different numbers by adding the following code at the end of the playground:
numberOfCombinations(4, setSize: 2) // 6
numberOfCombinations(6, setSize: 2) // 15
numberOfCombinations(6, setSize: 3) // 20
numberOfCombinations(6, setSize: 6) // 1Run the playground and you’ll see the results in the playground’s results pane.
You can calculate one of the numbers yourself to make sure you understand it.
What you’ve manually done here is exactly what Swift Algorithms provides natively. To see it in action, add the following code at the end of the playground:
let exampleCombinations = ["A", "B", "C"].combinations(ofCount: 2)
for set in exampleCombinations {
print(set)
}combinations(ofCount:) from Swift Algorithms calculates all the combinations of a sequence when choosing a certain number of them.
The results in the console log look like this:
["A", "B"]
["A", "C"]
["B", "C"]For a larger example, imagine you want to calculate all the possible match-ups for the clubs in the Premier League. Fortunately, there’s already a premierLeagueClubs constant in SampleData.swift:
let clubCombinations = premierLeagueClubs.combinations(ofCount: 2)Now get the count of all those possible combinations, and compare that result to the function you added in the beginning:
clubCombinations.count // 190
numberOfCombinations(premierLeagueClubs.count, setSize: 2) // 190Both values are the same. Since the Premier League has 20 clubs, then:
20 C 2 = 20 × 19 / 2 = 190Print the list of match-ups:
for teamups in clubCombinations {
print(teamups)
}It’ll show you a long list, and each is an array of two clubs:
["Arsenal", "Aston Villa"]
["Arsenal", "Brighton & Hove Albion"]
.
.
.
.
["West Bromwich Albion", "Wolverhampton Wanderers"]
["West Ham United", "Wolverhampton Wanderers"]That’s neat and handy right! Well, there’s more where that came from. Time to look at another similar algorithm.
Working With Permutations
The next item in the package is Permutations. It’s similar to combinations where you want to choose a certain number of items from a collection, but it’s concerned with the order of the items. This means the possible permutations for the group “A” and “B”, for a set of two items, are:
“A” + “B”
“B” + “A”
Following the same numerical example in combinations, the number of permutations of a group of five items choosing any 2, or “5 P 2” is:
5 × 4 × 3 × 2 × 1 / (3 × 2 × 1)Its mathematical equation is:
Factorial(5) / Factorial(5 - 2)The difference between the equations of permutations and combinations is the latter divides by the factorial of the set size. An example calculation is:
5 P 5 = Factorial(5) / Factorial(1) = (5 × 4 × 3 × 2 × 1) / 1 = 120On your Permutations playground page, add the following:
func numberOfPermutations(_ total: Int, setSize: Int) -> Double {
return total.factorial() / (total - setSize).factorial()
}Like before, this equation calculates the number of total results but not the results themselves. Add the following:
numberOfPermutations(4, setSize: 2) // 12
numberOfPermutations(6, setSize: 2) // 30
numberOfPermutations(6, setSize: 6) // 720Earlier, you calculated the number of match-ups between teams, but the result isn’t the actual number of matches, because every two teams play against each other twice — once on their home field and once as a visitor.
So in this example, permutations is the way to calculate the number of matches and what those matches are. The first team in each result is the home team, and the second one is the visitor.
Calculate how many matches there are:
let permutations = premierLeagueClubs.permutations(ofCount: 2)
permutations.count // 380This uses permutations(ofCount:) from Swift Algorithms. You can check the count is correct using the method you just added:
numberOfPermutations(premierLeagueClubs.count, setSize: 2) // 380The number of permutation results is twice the number of combination results, which makes sense, given that the teams play against one another twice.
Add the following to print the matches themselves:
for matches in permutations {
print(matches)
}The results in your log will look like this:
["Arsenal", "Aston Villa"]
["Arsenal", "Brighton & Hove Albion"]
.
.
.
["Wolverhampton Wanderers", "West Bromwich Albion"]
["Wolverhampton Wanderers", "West Ham United"]Working With Product
Next, you’ll learn about Product. The previous methods both created different variations within the same set, but this method is slightly different. It works with two collections — not one — and it gives you all the combinations of items in the first collection with items in the second collection. If that’s confusing, don’t worry; you’ll see an example in a moment.
On your Product playground page, add the following:
func doSomething(year: Int, season: String) {
print("In \(season) in the year \(year) something happened...")
}
for year in years {
for season in seasons {
doSomething(year: year, season: season)
}
}In the code above, years is a sequence from 2000 to 2020, seasons has the four seasons of the year, and you’re matching seasons with the years.
Note: years and seasons are both defined in SampleData.swift.
This code is simple to understand. But, it requires you to process all the items there and then within the nested for-loops. What if you want to save processing to later? That’s where using something Swift
Algorithms can do much better.
This is what Product does:
let productResults = product(years, seasons)
for (year, season) in productResults {
doSomething(year: year, season: season)
}Here you are using product(_:_) from Swift Algorithms to produce a result which can then be iterated whenever you want. In the simple example above, you do the same as the nested for loops, but crucially, you can see you have split the calculation of the product from the usage of the calculation’s results. Neat!
Working With Chunked
Chunked is the next algorithm, and it helps you break a collection down into smaller collections, processing each “chunk” in turn. You can define the way the main collection is broken into chunks however you wish.
To understand this better, try implementing it using sample data from the starter project.
marvelMoviesWithYears is an array of (String, Int) tuples containing a movie name and its year of release. The goal is to break this collection down into groups of movies released within the same year.
Start building a solution by adding the following to your Chunked playground page:
var groupedMovies: [[(String, Int)]] = []
var currentYear = marvelMoviesWithYears.first?.1var currentGroup: [(String, Int)] = []Here’s what each of these variables are for:
groupedMovies: Where you’ll store the final chunks.
currentYear: A temporary variable holding the year you’re currently checking.
currentGroup: The chunk you’re currently building.
Now, add the following code:
// 1for (movie, year) in marvelMoviesWithYears {
if currentYear == year {
// 2
currentGroup.append((movie, year))
} else {
// 3
groupedMovies.append(currentGroup)
currentGroup = [(movie, year)]
currentYear = year
}
}In the code above:
You’re iterating over the entire marvelMoviesWithYears collection.
If the item’s year is the same as the current value you’re comparing against, it belongs to the chunk you’re working on.
Otherwise, that chunk is complete; add it to the final result. In this case, prepare a new chunk with the new movie and use its year as your new comparison value.
After the loop concludes, groupedMovies contains all the chunks you want. Print them to see the results:
for group in groupedMovies {
print(group)
}[("Iron Man", 2008), ("The Incredible Hulk", 2008)]
[("Iron Man 2", 2010)]
.
.
[("Avengers: Infinity War", 2018), ("Ant-Man and the Wasp", 2018)]Swift Algorithms provides this implementation for you, so you don’t need to worry about any of its underlying details. All you need to define is the condition between an item and the one next to it.
Add the following to your playground:
let chunks = marvelMoviesWithYears.chunked { $0.1 == $1.1 }
for group in chunks {
print(group)
}This will produce exactly the same result. All you did was specify that the second property in the tuple of the first object equals that of the second object, and the method did all the work for you.
The code above uses Collection.chunked(by:), which takes a closure. There’s another variation, Collection.chunked(on:), that makes things simpler if your expression is a simple equality check. You would use it like this:
let sameChunks = marvelMoviesWithYears.chunked { $0.1 }In this form, the closure identifies which part of each object to use in the equality comparison.
Working With Chain
The opposite of breaking down a collection into chucks is to chain the chunks back together. The standard library already has Array.joined() for when the items in the array are sequences. So what’s new about chain(_:_:)?
On your Chain playground page, add the following:
let closedRange = 1...10let closedRange2 = 11...15let intArray = [11, 12, 13, 14, 15]The first two variables are two collections of type ClosedRange. The third is a simple integer array. If you try to join closedRange and intArray together, the compiler won’t be very happy:
let joinedLists = [closedRange, intArray].joined() // errorFor Array.joined() to work, all the collections in the array need to be of identical type. Either all elements are arrays, or closed ranges or whatever kind of sequence used, and they must match, so only this would work:
let joinedClosedRanges = [closedRange, closedRange2].joined()
for item in joinedClosedRanges {
print(item)
}But the new chain(_:_:) doesn’t have this restriction. Although it’s slightly limited by the number of sequences it can concatenate, it can accept different sequence types. Try the following in your playground:
let joinedItems = chain(closedRange, intArray)
for item in joinedItems {
print(item)
}As you can see, chain(_:_:) concatenated the two different sequence types successfully. However, the result from chain(_:_:) isn’t a single sequence. It’s a wrapper on top of the two collections that acts as a collection. It conforms to Collection, BidirectionalCollection and RandomAccessCollection if the two underlying sequences conform to them.
Working With Cycle
Sometimes you might want to repeat a sequence a number of times. For example you might want to repeat the numbers 1 through 5, ten times.
Add the following to your Cycle playground page:
var smallList = [1, 2, 3, 4, 5]
let repeatedAndJoined = repeatElement(smallList, count: 10).joined()
repeatedAndJoined.count // 50for item in repeatedAndJoined {
print(item)
}This code repeats a collection of the numbers 1 through 5, ten times with the call to repeatElement(_:count:). Then, it joins them up into one long collection with the call to joined(). Finally, it shows the count which we expect to be 50 and prints out the final collection.
Another way to do the same thing is to use the new Collection.cycled(times:). Add the following:
let cycles = smallList.cycled(times: 10)
cycles.count // 50for item in cycles {
print(item)
}The call to cycled(:) did the same thing! The implementation of Collection.cycled(times:) in the Swift Algorithms package repeats the elements and joins them, just like what you did before.
So what’s different about it? What if you want to have an infinite sequence? What if you want your small collection to repeat indefinitely? The first thing that would come to your mind is how such a sequence would be stored.
This is what’s beautiful about how Swift Algorithms make use of lazy collections. There’s another method called Collection.cycled(). It doesn’t take any number of repetitions and so when you iterate through the resulting collection, it will loop indefinitely.
Add the following to your playground:
let infiniteCycles = smallList.cycled()If you try to print the values here, it’ll keep writing numbers forever or until Xcode crashes.
This didn’t actually build a collection with a size of infinity! Instead, it created a wrapper above your collection that will keep going over the collection as long as you’re reading values from it.
Working With Unique
You’ve probably encountered many situations where you needed to get the unique values from a collection and you wrote code to do that. Now you can try to implement this with Swift Algorithms.
The playground comes with sample data in marvelProductionYears showing all the Marvel movies and the year they in which they were made. 2008 had two movies, so it’s in the collection twice. Try to filter that collection down to just a single item for each year that a Marvel movie was released.
Add the following to your Unique playground page:
var uniqueYears = Set<Int>(marvelProductionYears)
print(Array(uniqueYears))This is the simplest way to find the unique values from an array: Create a set from the array and you’re done. By definition, sets don’t store duplicate values. If you attempt to add an item that’s already present to the set, nothing will happen. This sounds easy, but there’s a small hole in this implementation. The values in the console are as follows:
[2017, 2013, 2014, 2008, 2016, 2018, 2019, 2012, 2011, 2015, 2010]Yours might be different. But as you can see, there is no order. The original array was ordered, but when you iterated over the set, it gave a completely different order. There’s a simple solution for this; add the following line to your playground:
print(marvelProductionYears.uniqued())Call uniqued() on any sequence and it’ll give you an array of only the unique values while maintaining the order of their appearance in the original sequence. The values in your console are ordered like this:
[2008, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]uniqued() has a constraint requirement on the element type: It must conform to Hashable. Otherwise, the sequence won’t have this method available.
Random Sampling
The standard library provides an easy way of getting a random value from a sequence: Sequence.randomElement(). But this may not be enough.
Consider for a moment that you want to watch some Marvel movies, chosen at random, but you don’t want to watch an older movie after a newer one.
Add the following code to your Random Sampling playground page:
var moviesToWatch: [String] = []
var numberOfMovies = 4for _ in 1...numberOfMovies {
moviesToWatch.append(marvelMovies.randomElement()!)
}
print(moviesToWatch)This code takes four random movies from the array. Sometimes the results will be fine, but most of the time they aren’t.
Consider the following possible result:
["Black Panther", "Iron Man", "Captain Marvel", "Thor: Ragnarok"]This isn’t the correct order of the movie releases. The correct order is:
["Iron Man", "Thor: Ragnarok", "Black Panther", "Captain Marvel"]There are simple ways to get a pseudo-random in-order sample. But there are also ways to implement this algorithm properly, which is what Swift Algorithms does for you.
So now, add the following:
print(marvelMovies.randomStableSample(count: numberOfMovies))Sequence.randomStableSample(count:) will choose count random items from the collection ensuring the order from the original collection is maintained.
Working With Indexed
It’s common to use enumerated() to iterate over a collection. It provides a sequence of pairs: an integer — which starts from zero — and a value.
Add the following code to your Indexed playground page:
let numbers = Array(1...50)
var matchingIntIndices: Set<Int> = []
for (i, number) in numbers.enumerated() {
if number.isMultiple(of: 20) {
matchingIntIndices.insert(i)
}
}
print(matchingIntIndices)In the code above, you created an array of integers with values from 1 to 50, and then you created a set to store the indices of the items that are multiples of 20.
The output of this code is:
[39, 19]This code works great as long as the array you’re looping on has a zero-based index. But if you’re going through an ArraySlice and want to get the proper indices, it won’t match. Add the following code to the same playground page:
matchingIntIndices = []
let subArray = numbers[10...]
for (i, number) in subArray.enumerated() {
if number.isMultiple(of: 20) {
matchingIntIndices.insert(i)
}
}
print(matchingIntIndices)Here you created a slice from the original array, starting from index 10 and continuing to the end of the array. The resulting indices are 9 and 29. These are the indices in the slice of the original collection.
You can use Swift Algorithms to help. Add the following to your playground:
var matchingIndices: Set<Int> = []
for (i, number) in subArray.indexed() {
if number.isMultiple(of: 20) {
matchingIndices.insert(i)
}
}
print(matchingIndices)
The output of this code is identical to the output in the previous example. Here you are using indexed() from Swift Algorithms to iterate the sub-array but maintaining the indices from the original array.
Working With Partition
Coming back to Marvel movies, say you want to watch them all in order, but break them down into Avengers movies and non-Avengers movies. The standard library already has a method for doing this: Collection.partition(by:). This reorders the collection by placing all the elements that pass the provided expression at the end of the collection, and it returns the index of the first item of those elements after reordering.
Try the following code on your Partition playground page:
var movies = marvelMoviesWithYears
let index = movies.partition { $0.0.contains("Avengers") }
for movie in movies[index...] {
print(movie)
}
You’ll see the following output:
("Avengers: Infinity War", 2018)
("Avengers: Age of Ultron", 2015)
("Avengers: Endgame", 2019)
("The Avengers", 2012)
Notice that after partitioning, the array of movies has lost its order. Fortunately, Swift Algorithms provides a different kind of partition method to keep things ordered.
Add the following to your playground:
var movies2 = marvelMoviesWithYears
let index2 = movies2.stablePartition { $0.0.contains("Avengers") }
for movie in movies2[index2...] {
print(movie)
}
The index will be the same as expected, but the partitions of the array are still ordered the same way they are in the original array.
It’s worth noting that if you use the first method on an already ordered collection and the expression is the same one used for the ordering, no swapping will occur and you’ll get the index of the item that satisfies the partitioning. Try the following:
var orderedMovies = marvelMoviesWithYears
let index3 = orderedMovies.partition { $0.1 > 2015 }
orderedMovies is still ordered even after calling the unstable partitioning method because the expression for the partitioning and the ordering criteria are the same. In this example, the index is 12.
You can find out if the collection is already partitioned using the new method, partitioningIndex(where:). If the resulting index is within the array, then it’s already ordered. But if it’s after the last element, then it isn’t.
Try the following two examples:
if marvelMoviesWithYears.partitioningIndex(where: { $0.0.contains("Avengers") }) < marvelMoviesWithYears.count {
print("Array is ordered")
} else {
print("Array is not properly ordered") // This will be printed
}
if marvelMoviesWithYears
.partitioningIndex(where: { $0.1 > 2015 }) < marvelMoviesWithYears.count {
print("Array is ordered") // This will be printed
} else {
print("Array is not properly ordered")
}
The first example will print "Array is not properly ordered", but the second one will print "Array is ordered".
Working With Rotate
The new Rotate feature let you rotate a collection by specifying which index to move to the beginning. To understand it, try it out and observe how the collection changes.
Add the following code to the Rotate playground page:
var numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
numbers.rotate(toStartAt: 3)
print(numbers) // [4, 5, 6, 7, 8, 9, 10, 1, 2, 3]With a collection of numbers from one to ten, calling rotate(toStartAt:) on the collection shift all elements to the left until the first element is the one at the index specified by the parameter. This algorithm is done in iterations which move the first item from the beginning to the end and shift all the rest to the left. The method returns the index of where the item that was first in the original collection is in the final, rotated collection. So in this example, the element "1" that was in index 0 is now in index 7.
When you rotate the entire collection, the number of elements in the collection minus the value you provide in toStartAt will be the expected index location of the first element before the rotation happens. And if you rotate by that number again, you'll return the collection to its original state:
numbers.rotate(toStartAt: 7) // returned back to normalprint(numbers) // [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]An alternative method lets you rotate a specific part of the collection. Say you want to rotate the first half of the collection and leave the second half untouched:
numbers.rotate(subrange: 0..<5, toStartAt: 2)
print(numbers) // [3, 4, 5, 1, 2, 6, 7, 8, 9, 10]This will rotate the elements from one to five and leave the elements from six to ten untouched.
Source: Raywenderlich
The Tech Platform






Comments