Selection Sort
- The Tech Platform

- Nov 2, 2020
- 3 min read
Updated: Aug 7, 2023
Selection Sort is a simple comparison-based sorting algorithm that divides the input array into two parts: a sorted part and an unsorted part. It repeatedly selects the minimum (or maximum, depending on the sorting order) element from the unsorted part of the array and places it at the end of the sorted part.
The algorithm works by iteratively finding the smallest element in the remaining unsorted part and swapping it with the first element of the unsorted part, effectively expanding the sorted part by one element in each iteration.
Here's how the Selection Sort algorithm works:
Start with the first element as the minimum (or maximum, depending on the sorting order) element in the array.
Compare this element with all other elements in the unsorted part of the array to find the actual minimum (or maximum) element.
Swap the minimum (or maximum) element found in STEP 2 with the first element of the unsorted part.
Move the boundary between the sorted and unsorted parts in one position to the right (by incrementing the index of the sorted part).
Repeat steps 1 to 4 until the entire array is sorted.
Selection Sort working:
This is our initial array A = [5, 2, 6, 7, 2, 1, 0, 3]
Step 1: Leftmost element of the unsorted part = A[0] (5)
Minimum element of the unsorted part = A[6] (0)
Swap A[0] and A[6] (5 and 0)
Array becomes: [0, 2, 6, 7, 2, 1, 5, 3]
Sorted part: [5]
Step 2: Leftmost element of the unsorted part = A[1] (2)
Minimum element of the unsorted part = A[5] (1)
Swap A[1] and A[5] (2 and 1)
Array becomes: [0, 1, 6, 7, 2, 2, 5, 3]
Sorted part: [5, 2]
Step 3: Leftmost element of the unsorted part = A[2] (6)
Minimum element of the unsorted part = A[4] (2)
Swap A[2] and A[4] (6 and 2)
Array becomes: [0, 1, 2, 7, 6, 2, 5, 3]
Sorted part: [5, 2, 6]
Step 4: Leftmost element of the unsorted part = A[3] (7)
Minimum element of the unsorted part = A[5] (2)
Swap A[3] and A[5] (7 and 2)
Array becomes: [0, 1, 2, 2, 6, 7, 5, 3]
Sorted part: [5, 2, 6, 7]
Step 5: Leftmost element of the unsorted part = A[4] (6)
Minimum element of the unsorted part = A[7] (3)
Swap A[4] and A[7] (6 and 3)
Array becomes: [0, 1, 2, 2, 3, 7, 5, 6]
Sorted part: [5, 2, 6, 7, 3]
Step 6: Leftmost element of the unsorted part = A[5] (7)
Minimum element of the unsorted part = A[6] (5)
Swap A[5] and A[6] (7 and 5)
Array becomes: [0, 1, 2, 2, 3, 5, 7, 6]
Sorted part: [5, 2, 6, 7, 3, 5]
Step 7: Leftmost element of the unsorted part = A[6] (7)
Minimum element of the unsorted part = A[7] (6)
Swap A[6] and A[7] (7 and 6)
Array becomes: [0, 1, 2, 2, 3, 5, 6, 7]
Sorted part: [5, 2, 6, 7, 3, 5, 7]
Pseudocode
FindMinIndex:
FindMinIndex(Arr[], start, end)
min_index = start
FOR i from (start + 1) to end:
IF Arr[i] < Arr[min_index]:
min_index = i
END of IF
END of FOR
Return min_indexThe FindMinIndex function is a helper function used by the SelectionSort function to find the index of the minimum element in the array from the given start index to the end index.
The time complexity of the FindMinIndex function is O(n), where "n" is the number of elements in the array. It iterates through the array once to find the minimum element's index.
Therefore,
Time complexity: O(n)
Space complexity: O(1)
Selection Sort:
SelectionSort(Arr[], arr_size):
FOR i from 1 to arr_size:
min_index = FindMinIndex(Arr, i, arr_size)
IF i != min_index:
swap(Arr[i], Arr[min_index])
END of IF
END of FORThe SelectionSort function uses the FindMinIndex function to find the minimum element's index in the unsorted part of the array and swaps it with the first element of the unsorted part. This process is repeated for each element in the array until the entire array is sorted.
The time complexity of the SelectionSort function is O(n^2), as it involves two nested loops. In the worst case, the outer loop runs "n" times, and for each iteration of the outer loop, the inner loop (FindMinIndex function) runs approximately "n/2" times on average.
Total iterations = (n – 1) + (n – 2) + . . . + 1 = (n * (n – 1)) / 2 = (n2 – n) / 2
Therefore,
Time complexity: O(n2)
Space complexity: O(1)
Both functions use O(1) space as they do not require any additional memory that scales with the input size "n".
Overall, the Selection Sort algorithm is a simple sorting algorithm with a time complexity of O(n^2), making it inefficient for large datasets. For larger arrays, more efficient sorting algorithms like Merge Sort or Quick Sort are generally preferred.









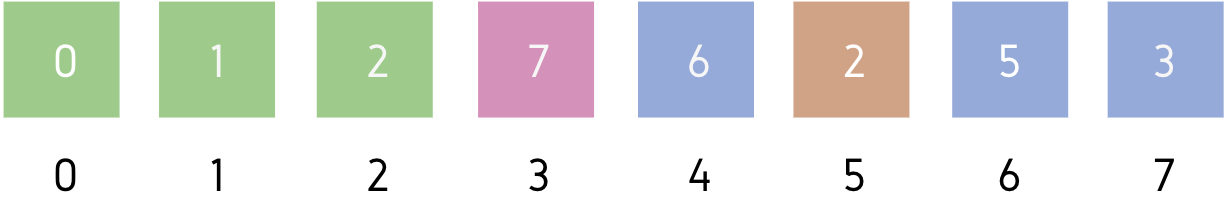

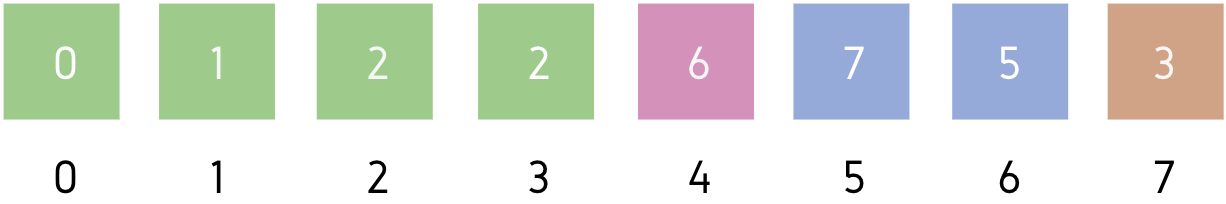

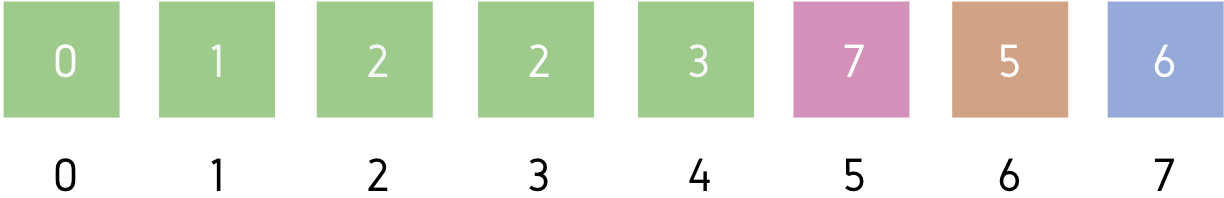

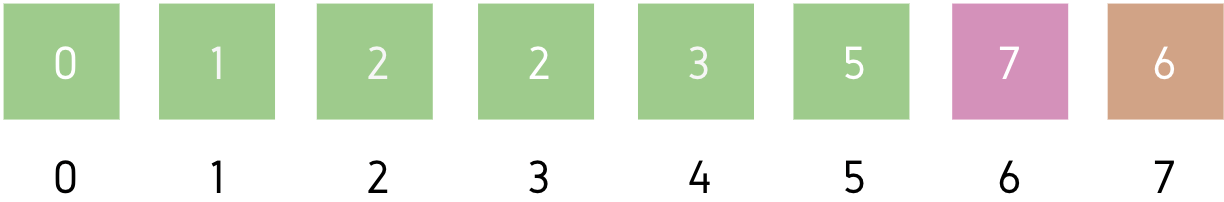






Comments