Bubble Sort Algorithm
- The Tech Platform

- Nov 2, 2020
- 7 min read
Updated: Aug 8, 2023
Bubble sort, also known as a comparison sort, is a simple yet rudimentary sorting algorithm. It iterates through a list multiple times, comparing adjacent elements, and performing swaps if they are found to be in the incorrect order. Despite its straightforward nature, this algorithm's efficiency is notably lacking. Nevertheless, its significance lies in its role as a foundational concept in the realm of sorting algorithms.
Application:
Here are some practical applications of the bubble sort algorithm:
Educational Tool: As mentioned earlier, bubble sort serves as a foundational learning tool for students to understand sorting algorithms. It's simplicity and visual nature make it an excellent starting point for teaching basic sorting concepts.
Small Dataset Sorting: While bubble sort is inefficient for larger datasets, it can still be used for small datasets where performance is not a critical concern. Its ease of implementation and minimal memory usage can be advantageous in such cases.
Testing and Debugging: Bubble sort's simplicity makes it useful for testing and debugging other, more complex sorting algorithms. Since it's easy to implement and understand, it can be used to verify the correctness of sorting algorithms by comparing their results to the known outcome of bubble sort.
Detecting Nearly Sorted Lists: Bubble sort's adaptive nature (being more efficient when dealing with nearly sorted lists) can be used to identify lists that are mostly ordered with only a few elements out of place. In such cases, bubble sorting can complete quickly, offering a simple method to identify pre-sorted or partially sorted data.
Teaching Sorting Concepts: Beyond its educational utility, bubble sort can be used to demonstrate sorting concepts in workshops, coding tutorials, and programming courses. It allows beginners to grasp the idea of sorting and the importance of algorithmic efficiency.
Historical Understanding: Bubble sort has historical significance in the evolution of computer science. Learning about bubble sort helps individuals appreciate how algorithms have developed over time and why more efficient algorithms were developed to overcome their limitations.
Algorithmic Analysis: Studying bubble sort's time complexity (both average and worst-case scenarios) provides insights into understanding algorithm analysis and comparisons between different sorting techniques.
Sorting Small, Nearly Sorted Datasets: When dealing with datasets that are already nearly sorted or have a limited number of elements out of place, bubble sort's adaptiveness can offer reasonable performance compared to other algorithms.
Understanding Bubble Sort's Mechanics: Bubble sort finds its primary application in education, serving as a didactic tool to help students grasp the fundamental principles of sorting algorithms.
Detecting List Order: One of its practical uses is determining whether a given list is already sorted. In the best-case scenario where the list is already sorted, the time complexity of bubble sort reduces to O(n).
Real-Life Analogous Scenario: To illustrate bubble sort's approach, envision a real-life scenario where individuals queue up, aiming to arrange themselves by height in ascending order. As in the algorithm, people in the queue interchange their positions iteratively until the queue is correctly ordered based on increasing heights.
Despite its inefficiency, particularly for large datasets, bubble sort remains a pivotal learning tool due to its simple design and tangible representation, making it an indispensable stepping stone for understanding the foundational concepts of sorting algorithms.
Pseudocode of Bubble Sort Algorithm
bubbleSort( Arr[], totat_elements)
for i = 0 to total_elements - 1 do:
swapped = false
for j = 0 to total_elements - i - 2 do:
/* compare the adjacent elements */
if Arr[j] > Arr[j+1] then
/* swap them */
swap(Arr[j], Arr[j+1])
swapped = true
end if
end for
/*if no number was swapped that means
array is sorted now, break the loop.*/
if(not swapped) then
break
end if
end for
endAlgorithm Overview
The bubble sort algorithm is based on a simple principle: comparing adjacent elements in an array and swapping them if their order is incorrect (e.g., for ascending order: a[i] > a[j] where 1 <= i < j <= size of the array, and vice versa for descending order). The process involves multiple passes through the array, gradually placing the largest elements in their correct positions.
Step-by-Step Explanation:
Consider an array of length n. To sort this array, the following procedure is performed for n - 1 passes:
In the first pass, the largest element is swapped to its rightful place at the far right end of the array.
In the second pass, the second largest element is swapped to the second-to-last position, and so on.
This pattern continues until the (n - 1)th pass, where the (n - 1)th largest element is placed correctly in the array by swapping.
Mathematical Interpretation:
Mathematically, during the ith pass, at least one element from the first (n - i + 1) elements will find its proper position. This element happens to be the ith largest (for 1 <= i <= n - 1) element of the array. This conclusion can be drawn because, in the ith pass, during the jth iteration (where 1 <= j <= n - i), the comparison a[j] > a[j + 1] is carried out. If a[j] is indeed the largest element within the range [1, n - i + 1], it will always be greater than a[j + 1]. Consequently, a[j] will be swapped with a[j + 1], effectively moving the largest element to the proper position.
This process of swapping and gradually positioning the largest elements within their respective ranges continues until the ith largest element eventually takes its place at the (n - i + 1)th position of the array. This method ensures that the array is sorted incrementally in each pass, leading to the final sorted arrangement.
Bubble Sort Example:
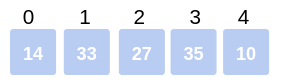
Consider the given array: Arr = 14, 33, 27, 35, 10. Our objective is to utilize the bubble sort algorithm to arrange this array in ascending order.
First Pass:
We start by examining the first and second elements, Arr[0] and Arr[1]. Since 14 is not greater than 33, no swapping occurs, and the array remains unchanged.
We proceed to the second and third elements, Arr[1] and Arr[2]. As 33 is greater than 27, we swap these elements, resulting in the array:
Arr = 14, 27, 33, 35, 10.
Continuing, we move to the third and fourth elements, Arr[2] and Arr[3]. Since 33 is not greater than 35, no swapping takes place, and the array remains the same.
Finally, we analyze the fourth and fifth elements, Arr[3] and Arr[4]. As 35 is greater than 10, we swap these elements, leading to the array:
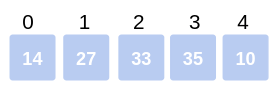
Arr = 14, 27, 33, 10, 35.
This concludes the first pass, during which the largest element reaches its final (last) position.
Second Pass:
We start again with the first and second elements, Arr[0] and Arr[1]. Since 14 is not greater than 27, no swapping occurs, and the array remains unaltered.
Moving on to the second and third elements, Arr[1] and Arr[2], we observe that 27 is not greater than 33. Consequently, no swapping is performed, and the array stays the same.
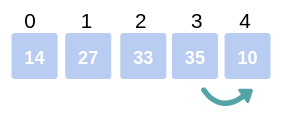
Lastly, we consider the third and fourth elements, Arr[2] and Arr[3]. Since 33 is greater than 10, we swap these elements, resulting in the array:
Arr = 14, 27, 10, 33, 35.
The second pass concludes with the second largest element occupying its correct position in the array.
The pattern continues as follows for subsequent passes:
After the third pass, the third largest element will reside in the third-to-last position in the array.
.
In the ith pass, the ith largest element will be placed at the ith-to-last position in the array.
After the nth pass, the nth largest element (smallest element) will occupy the first position in the array, where 'n' represents the size of the array.
Upon completing all the passes, the array is observed to be sorted in ascending order. Thus, the sorted array will appear as:
Arr = 10, 14, 27, 33, 35.
Implementation Of Bubble Sort in Different Programming Languages
1. Bubble Sort in C
#include<stdio.h>
int main() {
int arr[] = {5, 6, 2 ,6, 9, 0, -1}, n = 7, i, j;
for(i = 0; i < n - 1; ++i) {
int swapped = 0;
for(j = 0; j < (n - i - 1); ++j)
if(arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp; swapped = 1;
}
if(!swapped) break;
}
printf("\nArray after sorting: ");
for(i = 0; i < n; ++i)
printf("%d ", arr[i]);
return 0;
}2. Bubble Sort in C++
#include <iostream>
#include <vector>
using namespace std;
void BubbleSort (vector<int> &arr, int n)
{
for (int i = 0; i < n - 1; ++i)
{
bool swapped = false;
for (int j = 0; j < n - i - 1; ++j)
{
if (arr[j] > arr[j+1]) //check if adjacent element is
//not in order
{
swap(arr[j], arr[j + 1]);
swapped = true;
}
}
// Value at n-i-1 will be maximum of all the values below this index.
if(!swapped)
break;
}
}
int main()
{
vector<int> arr = {5, 6, 2, 6, 9, 0, -1};
int n = 7;
BubbleSort(arr, n);
// Display the sorted data.
cout << "\nSorted Data: ";
for (i = 0; i < n; i++)
Cout << arr[i] << “ “;
return 0;
}3. Bubble Sort in Java
import java.util.Scanner;
class BubbleSort {
public static void main(String []args) {
int n;
Scanner in = new Scanner(System.in);
System.out.println("Input number of integers to sort");
n = in.nextInt();
int array[] = new int[n];
System.out.println("Enter " + n + " integers");
for (int i = 0; i < n; i++)
array[i] = in.nextInt();
for (int i = 0; i < n - 1; i++) {
Boolean swapped = false;
for (int j = 0; j < n - i - 1; j++) {
if (array[j] > array[j+1]) /* For descending order use < */
{
int temp = array[j];
array[j]= array[j+1];
array[j+1] = temp;
swapped = true;
}
}
if(!swapped)
break;
}
System.out.println("Sorted list of numbers:");
for (int i = 0; i < n; i++)
System.out.println(array[i]);
}
}4. Bubble Sort in Python
def bubble_sort(arr):
for i in range(len(arr) - 1):
swapped = False
for j in range(0, len(arr) - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swapped = True
if not swapped:
return
arr = [int(x) for x in input(‘Enter numbers: ’).split()]
bubble_sort(arr)
print('Sorted list: ', end='')
print(arr)Time Complexity of Bubble Sort
Best Case Scenario:
In the best-case scenario, the array is already sorted. As a result, no swaps are needed during the first iteration, and the loop breaks after that initial pass. Thus, the time complexity in the best case is O(n), as the algorithm only needs to traverse through all the elements once.
Worst and Average Case Scenario:
For both the worst and average cases, Bubble Sort follows a specific pattern. In the 1st pass, n-1 comparisons are performed. In the 2nd pass, n-2 comparisons are done, and so on. Ultimately, the total number of comparisons can be calculated as the sum of the series from 1 to n-1:
Sum = (n-1) + (n-2) + (n-3) + ... + 3 + 2 + 1
This sum can be simplified using the formula for the sum of an arithmetic series: Sum = n(n-1)/2.
Hence, the time complexity of Bubble Sort in the worst and average cases is of the order n^2, represented as O(n^2).
Space Complexity of Bubble Sort:
The space complexity of Bubble Sort is O(1), indicating that the algorithm requires only a constant amount of additional memory space. This space is used primarily for a temporary variable during swapping. Regardless of the size of the input array, the amount of memory used remains constant, making the space complexity O(1).









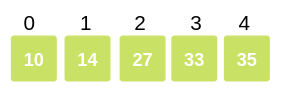



Comments