Binary Search Algorithm

Binary Search Algorithm is a search technique that is used to sort the list. To search for an element from the list using Binary Search Algorithm, we must ensure that the list is sorted.

Binary Search Technique follows the divide and conquers approach in which the list is divided into two halves, and then the center element is compared with all the middle elements of the list.

Algorithm:

STEP 1: Set beg = lower_bound, end = upper_bound, pos = - 1

STEP 2: Repeat steps 3 and 4 while beg <=end

STEP 3: Set mid = (beg + end)/2

STEP 4: if a[mid] = val

set pos = mid

print pos

go to step 6

else if a[mid] > val

set end = mid - 1

else

set beg = mid + 1

[end of if]

[end of loop]

STEP 5: if pos = -1

print "value is not present in the array"

[end of if]

STEP 6: Exit.

How it Works?

The general steps for both methods are discussed below.

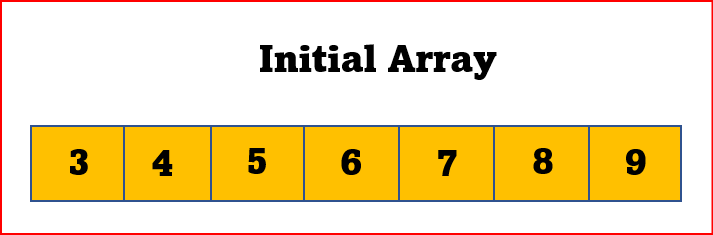
STEP 1: The array in which searching is to be performed is: Let x = 4 be the element to be searched.

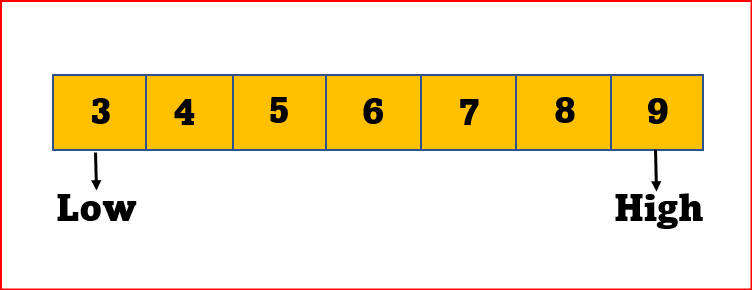
STEP 2: Set two pointers low and high at the lowest and the highest positions respectively.

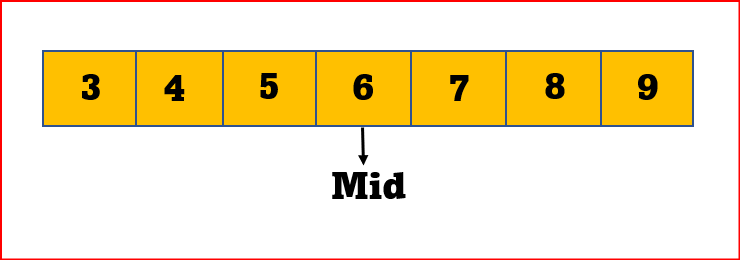
STEP 3: Find the middle element mid of the array ie. arr[(low + high)/2] = 6.

STEP 4: If x == mid, then return mid.Else, compare the element to be searched with m.

STEP 5: If x > mid, compare x with the middle element of the elements on the right side of mid. This is done by setting low to low = mid + 1.

STEP 6: Else, compare x with the middle element of the elements on the left side of mid. This is done by setting high to high = mid - 1.

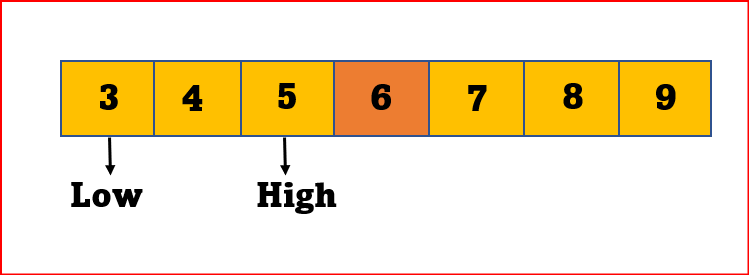
STEP 7: Repeat steps 3 to 6 until low meets high.

STEP 8: x = 4 is found.

Example:

def binarySearch(array, x, low, high):

    if high >= low:

        mid = low + (high - low)//2

        # If found at mid, then return it
        if array[mid] == x:
            return mid

        # Search the left half
        elif array[mid] > x:
            return binarySearch(array, x, low, mid-1)

        # Search the right half
        else:
            return binarySearch(array, x, mid + 1, high)

    else:
        return -1


array = [3, 4, 5, 6, 7, 8, 9]
x = 8

result = binarySearch(array, x, 0, len(array)-1)

if result != -1:
    print("Element is present at index " + str(result))
else:
    print("Not found")

Output:

Time Complexity

Best Case Complexity - In Binary search, the best case occurs when the element to search is found in the first comparison, i.e., when the first middle element itself is the element to be searched. The best-case time complexity of Binary search is O(1).

Average Case Complexity - The average case time complexity of Binary search is O(logn).

Worst Case Complexity - In Binary search, the worst case occurs, when we have to keep reducing the search space till it has only one element. The worst-case time complexity of Binary search is O(logn).