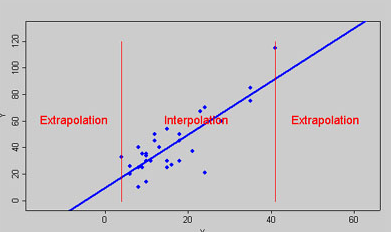
Interpolation is a mathematical technique to estimate values of an unknown function f(x) for specific arguments x in some interval [a, b], when a number of observed values f(x) are available within that interval. If you want to estimate values of f(x) when x is outside [a, b], the problem is then called extrapolation. The methodology being used could be OLS (ordinary least squares) and can provide error bounds on the estimated values, for instance using model-free confidence intervals or other techniques.
Prediction - more specifically predictive modeling - is a technique based on statistical modeling to essentially compute the estimates that you can get via extrapolation. Likewise, it provides confidence bands for the estimated values.
So what is the difference between extrapolation and prediction? Do they provide different results? When is it best to use extrapolation versus prediction? In my opinion, there is no difference, it's just a question of context: whether the people doing the analysis call themselves mathematician or statistician.
What do you think?
DSC Resources
Career: Training | Books | Cheat Sheet | Apprenticeship | Certification | Salary Surveys | Jobs
Knowledge: Research | Competitions | Webinars | Our Book | Members Only | Search DSC
Buzz: Business News | Announcements | Events | RSS Feeds
Misc: Top Links | Code Snippets | External Resources | Best Blogs | Subscribe | For Bloggers
Source:Paper.li