Insertion Sort Implementation In C

#include <stdio.h>
#include <stdbool.h>

#define MAX 7	//defining size of our array

int intArray[MAX] = {4,6,3,2,1,9,7};

void printline(int count) {
  int i;

  for(i = 0;i < count-1;i++) {
     printf("=");
  }

  printf("=\n");
}

void display() {
  int i;
  printf("[");

  // navigate through all items 
  for(i = 0;i < MAX;i++) {
     printf("%d ",intArray[i]);
  }

  printf("]\n");
}

void insertionSort() {

  int valueToInsert;
  int holePosition;
  int i;
 
  // loop through all numbers 
  for(i = 1; i < MAX; i++) { 

     // select a value to be inserted. 
     valueToInsert = intArray[i];

     // select the hole position where number is to be inserted 
     holePosition = i;

     // check if previous no. is larger than value to be inserted 
     while (holePosition > 0 && intArray[holePosition-1] > valueToInsert) {
        intArray[holePosition] = intArray[holePosition-1];
        holePosition--;
        printf(" item moved : %d\n" , intArray[holePosition]);
     }

     if(holePosition != i) {
        printf(" item inserted : %d, at position : %d\n" , valueToInsert,holePosition);
        // insert the number at current hole
        intArray[holePosition] = valueToInsert;
     }

     printf("Iteration %d#:",i);
     display();

  } 
}

void main() {
  printf("Input Array: ");
  display();
  printline(50);
  insertionSort();
  printf("Output Array: ");
  display();
  printline(50);
}

Characteristics of Insertion Sort:

1. It is efficient for smaller data sets, but very inefficient for larger lists.

2. Insertion Sort is adaptive, that means it reduces its total number of steps if a partially sorted array is provided as input, making it efficient.

3. It is better than Selection Sort and Bubble Sort algorithms.

4. Its space complexity is less. Like bubble Sort, insertion sort also requires a single additional memory space.

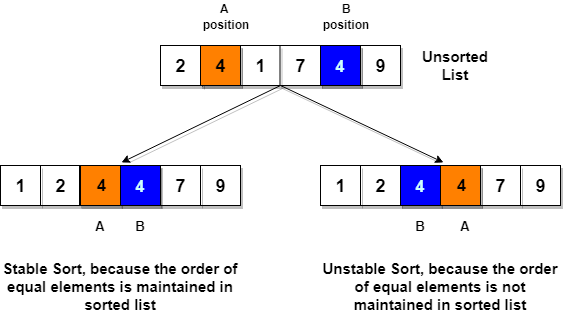
5. It is a stable sorting technique, as it does not change the relative order of elements which are equal.

Complexity Analysis of Insertion Sort

Even though insertion sort is efficient, still, if we provide an already sorted array to the insertion sort algorithm, it will still execute the outer for loop, thereby requiring n steps to sort an already sorted array of n elements, which makes its best case time complexity a linear function of n.

Worst Case Time Complexity [ Big-O ]: O(n2)

Best Case Time Complexity [Big-omega]: O(n)

Average Time Complexity [Big-theta]: O(n2)

Space Complexity: O(1)

Resources: Studytonight.com

Interviewbit.com

The Tech Platform

www.thetechplatform.com