Introduction to Genetic Algorithm
- The Tech Platform

- Jan 22, 2021
- 5 min read
Genetic Algorithm (GA) is a search-based optimization technique based on the principles of Genetics and Natural Selection. It is frequently used to find optimal or near-optimal solutions to difficult problems which otherwise would take a lifetime to solve. It is frequently used to solve optimization problems, in research, and in machine learning.
In GAs, we have a pool or a population of possible solutions to the given problem. These solutions then undergo recombination and mutation (like in natural genetics), producing new children, and the process is repeated over various generations. Each individual (or candidate solution) is assigned a fitness value (based on its objective function value) and the fitter individuals are given a higher chance to mate and yield more “fitter” individuals. This is in line with the Darwinian Theory of “Survival of the Fittest”.
In this way we keep “evolving” better individuals or solutions over generations, till we reach a stopping criterion.
Genetic Algorithms are sufficiently randomized in nature, but they perform much better than random local search (in which we just try various random solutions, keeping track of the best so far), as they exploit historical information as well.
Basic Terminology
Before beginning a discussion on Genetic Algorithms, it is essential to be familiar with some basic terminology which will be used throughout this tutorial.
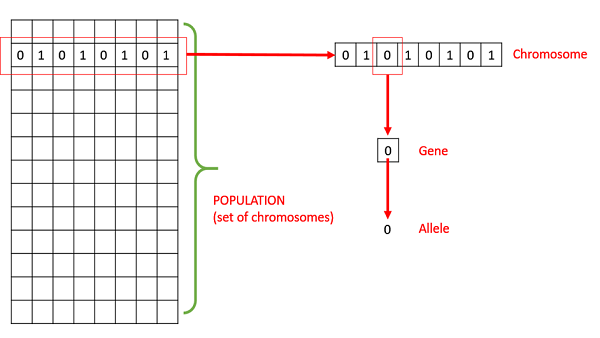
Population − It is a subset of all the possible (encoded) solutions to the given problem. The population for a GA is analogous to the population for human beings except that instead of human beings, we have Candidate Solutions representing human beings.
Chromosomes − A chromosome is one such solution to the given problem.
Gene − A gene is one element position of a chromosome.
Allele − It is the value a gene takes for a particular chromosome.
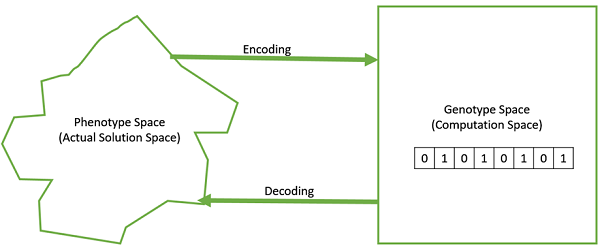
Genotype − Genotype is the population in the computation space. In the computation space, the solutions are represented in a way which can be easily understood and manipulated using a computing system.
Phenotype − Phenotype is the population in the actual real world solution space in which solutions are represented in a way they are represented in real world situations.
Decoding and Encoding − For simple problems, the phenotype and genotype spaces are the same. However, in most of the cases, the phenotype and genotype spaces are different. Decoding is a process of transforming a solution from the genotype to the phenotype space, while encoding is a process of transforming from the phenotype to genotype space. Decoding should be fast as it is carried out repeatedly in a GA during the fitness value calculation. For example, consider the 0/1 Knapsack Problem. The Phenotype space consists of solutions which just contain the item numbers of the items to be picked. However, in the genotype space it can be represented as a binary string of length n (where n is the number of items). A 0 at position x represents that xth item is picked while a 1 represents the reverse. This is a case where genotype and phenotype spaces are different.
Fitness Function − A fitness function simply defined is a function which takes the solution as input and produces the suitability of the solution as the output. In some cases, the fitness function and the objective function may be the same, while in others it might be different based on the problem.
Genetic Operators − These alter the genetic composition of the offspring. These include crossover, mutation, selection, etc.
Basic Structure
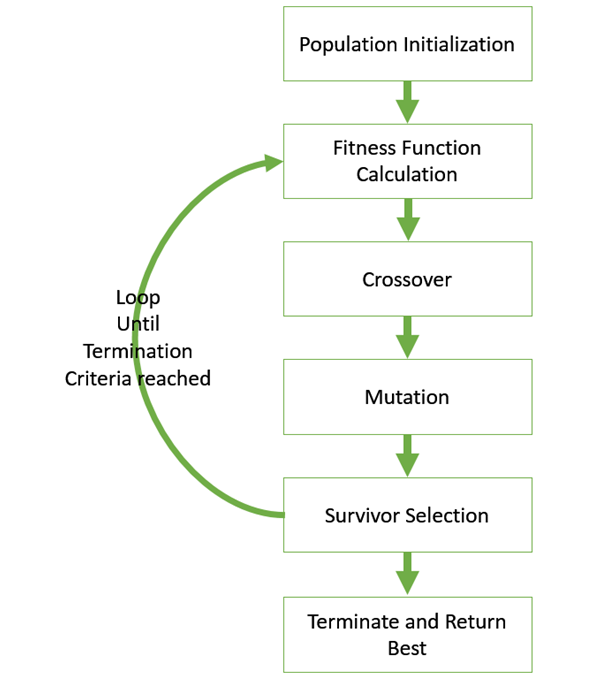
The basic structure of a GA is as follows −
We start with an initial population (which may be generated at random or seeded by other heuristics), select parents from this population for mating. Apply crossover and mutation operators on the parents to generate new off-springs. And finally these off-springs replace the existing individuals in the population and the process repeats. In this way genetic algorithms actually try to mimic the human evolution to some extent.
Each of the following steps are covered as a separate chapter later in this tutorial.
A generalized pseudo-code for a GA is explained in the following program −
GA()
initialize population
find fitness of population
while (termination criteria is reached) do
parent selection
crossover with probability pc
mutation with probability pm
decode and fitness calculation
survivor selection
find best
return bestAdvantages of GAs
GAs have various advantages which have made them immensely popular. These include −
Does not require any derivative information (which may not be available for many real-world problems).
Is faster and more efficient as compared to the traditional methods.
Has very good parallel capabilities.
Optimizes both continuous and discrete functions and also multi-objective problems.
Provides a list of “good” solutions and not just a single solution.
Always gets an answer to the problem, which gets better over the time.
Useful when the search space is very large and there are a large number of parameters involved.
Limitations of GAs
Like any technique, GAs also suffer from a few limitations. These include −
GAs are not suited for all problems, especially problems which are simple and for which derivative information is available.
Fitness value is calculated repeatedly which might be computationally expensive for some problems.
Being stochastic, there are no guarantees on the optimality or the quality of the solution.
If not implemented properly, the GA may not converge to the optimal solution.
Application
Genetic Algorithms are primarily used in optimization problems of various kinds, but they are frequently used in other application areas as well.
In this section, we list some of the areas in which Genetic Algorithms are frequently used. These are −
Optimization − Genetic Algorithms are most commonly used in optimization problems wherein we have to maximize or minimize a given objective function value under a given set of constraints. The approach to solve Optimization problems has been highlighted throughout the tutorial.
Economics − GAs are also used to characterize various economic models like the cobweb model, game theory equilibrium resolution, asset pricing, etc.
Neural Networks − GAs are also used to train neural networks, particularly recurrent neural networks.
Parallelization − GAs also have very good parallel capabilities, and prove to be very effective means in solving certain problems, and also provide a good area for research.
Image Processing − GAs are used for various digital image processing (DIP) tasks as well like dense pixel matching.
Vehicle routing problems − With multiple soft time windows, multiple depots and a heterogeneous fleet.
Scheduling applications − GAs are used to solve various scheduling problems as well, particularly the time tabling problem.
Machine Learning − as already discussed, genetics based machine learning (GBML) is a niche area in machine learning.
Robot Trajectory Generation − GAs have been used to plan the path which a robot arm takes by moving from one point to another.
Parametric Design of Aircraft − GAs have been used to design aircrafts by varying the parameters and evolving better solutions.
DNA Analysis − GAs have been used to determine the structure of DNA using spectrometric data about the sample.
Multimodal Optimization − GAs are obviously very good approaches for multimodal optimization in which we have to find multiple optimum solutions.
Traveling salesman problem and its applications − GAs have been used to solve the TSP, which is a well-known combinatorial problem using novel crossover and packing strategies.
Source: Tutorialpoint






Comments