How to implement Radix Sort in Java

The Radix sort, like counting sort and bucket sort, is an integer-based algorithm (I mean the values of the input array are assumed to be integers). Hence radix sort is among the fastest sorting algorithms around, in theory. It is also one of the few O(n) or linear time sorting algorithms along with the Bucket and Counting sort. The particular distinction for radix sort is that it creates a bucket for each cipher (i.e. digit); as such, similar to bucket sort, each bucket in radix sort must be a growable list that may admit different keys.

For decimal values, the number of buckets is 10, as the decimal system has 10 numerals/cyphers (i.e. 0,1,2,3,4,5,6,7,8,9). Then the keys are continuously sorted by significant digits.

Time Complexity of radix sort in the best case, average case, and worst case is O(k*n) where k is the length of the longest number, and n is the size of the input array.

Note: if k is greater than log(n) then a n*log(n) algorithm would be a better fit. In reality, we can always change the Radix to make k less than log(n).

Java program to implement Radix sort algorithm

Before solving this problem or implementing a Radix Sort Algorithm, let's first get the problem statement right: Problem Statement: Given a disordered list of integers, rearrange them in the natural order. Sample Input: {18,5,100,3,1,19,6,0,7,4,2} Sample Output: {0,1,2,3,4,5,6,7,18,19,100} Solution Here is a sample program to implement the Radix sort algorithm in Java

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/** Java Program sort an integer array using radix sort algorithm.
 * input: [180, 50, 10, 30, 10, 29, 60, 0, 17, 24, 12]
 * output: [0, 10, 10, 12, 17, 24, 29, 30, 50, 60, 180]
 ** Time Complexity of Solution:
 *   Best Case O(k*n); Average Case O(k*n); Worst Case O(k*n),
 *   where k is the length of the longest number and n is the*   size of the input array.
 **   Note: if k is greater than log(n) then an n*log(n) algorithm would be a
 *         better fit. In reality we can always change the radix to make k
 *         less than log(n).
 **/

public class Main {

  public static void main(String[] args) {

    System.out.println("Radix sort in Java");
    int[] input = { 181, 51, 11, 33, 11, 39, 60, 2, 27, 24, 12 };

    System.out.println("An Integer array before sorting");
    System.out.println(Arrays.toString(input));

    // sorting array using radix Sort Algorithm
    radixSort(input);

    System.out.println("Sorting an int array using radix sort algorithm");
    System.out.println(Arrays.toString(input));

  }

  /*** Java method to sort a given array using radix sort algorithm
   ** @param input
   */
  public static void radixSort(int[] input) {
    final int RADIX = 10;
    
    // declare and initialize bucket[]
    List<Integer>[] bucket = new ArrayList[RADIX];
    
    for (int i = 0; i < bucket.length; i++) {
      bucket[i] = new ArrayList<Integer>();
    }

    // sort
    boolean maxLength = false;
    int tmp = -1, placement = 1;
    while (!maxLength) {
      maxLength = true;
      
      // split input between listsfor (Integer i : input) {
        tmp = i / placement;
        bucket[tmp % RADIX].add(i);
        if (maxLength && tmp > 0) {
          maxLength = false;
        }
      }
      
      // empty lists into input array
      int a = 0;
      for (int b = 0; b < RADIX; b++) {
        for (Integer i : bucket[b]) {
          input[a++] = i;
        }
        bucket[b].clear();
      }
      
      // move to next digit
      placement *= RADIX;
    }
  }
}

Output
Radix sort in Java
An Integer array before sorting
[181, 51, 11, 33, 11, 39, 60, 2, 27, 24, 12]
Sorting an int array using radix sort algorithm
[2, 11, 11, 12, 24, 27, 33, 39, 51, 60, 181]

Here is another example of sorting a list of an integer using Radix sort, just in case If you haven't got the concept of how Radix sort works:

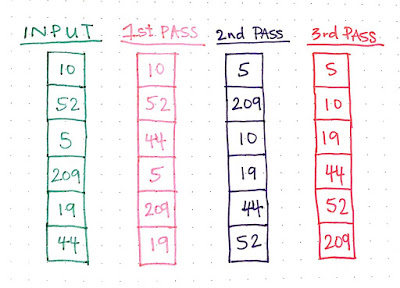
Problem Statement:

Sort the list of numbers 10, 52, 5, 209, 19, and 44 using the Radix sort algorithm:

Solution:

That's all about how to sort an integer array using radix sort in Java. Along with Counting Sort and Bucket sort, it is also an O(n) sorting algorithm. These algorithms are not general-purpose and you cannot use them to sort any object like String, Employee, etc. They are best suited for a small range of known integer values but they provide awesome performance.

Source: Java67

The Tech Platform

www.thetechplatform.com